Notebook Series

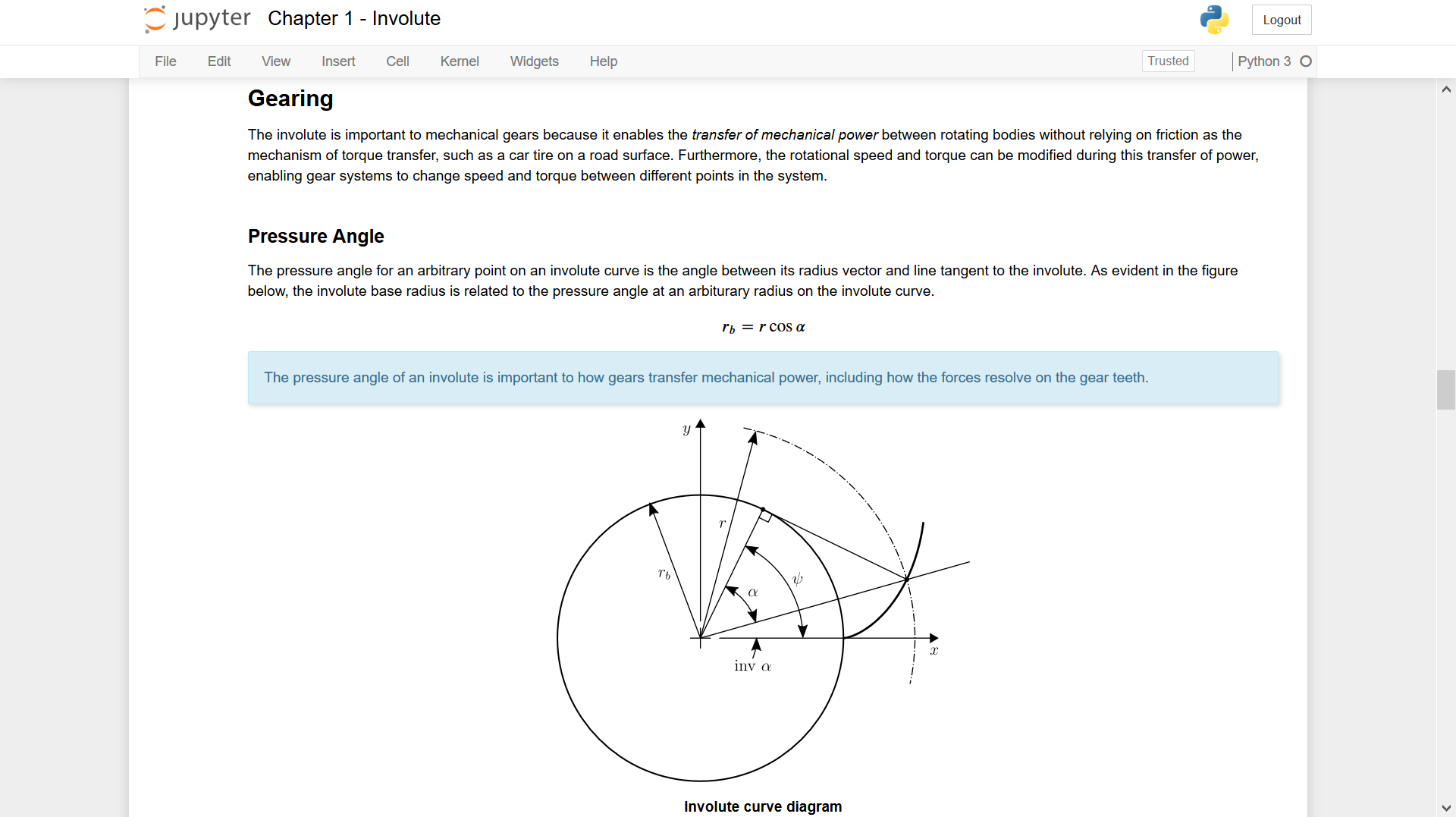
Mathematical review of the involute curve and its significance to mechanical gear systems. An involute, specifically a circle involute, is a geometric curve that can be described by the trace of unwrapping a taut string which is tangent to a circle, known as the base circle. The circle involute has attributes that are critically important to the application of mechanical gears.

Geometry of spur gears and spur gear pairs is reviewed. Methods and examples of geometric design are reviewed for spur gear pairs, given constraints on ratio, center distance, and clearances. For a given module and center distance, a gear pair is designed to achieve a desired gear ratio, while the gear geometry is constrained to certain criteria.

Geometry of helical gears and helical gear meshes is reviewed. Helical gears have similarities with spur gears, but fundamental differences do exist. A helical gear is similar to a spur gear with an applied twist along its axial axis. This notebook reviews geometric attributes of helical gears and their significance to helical gear mesh operation.

Geometric layout design of planetary geartrains with spur and helical gears is reviewed. Typical planetary gearsets have a sun gear, ring gear, and multiple planet gears on a carrier component. Spur or helical gears are used for a planetary gearset, with each type having advantages. Planetary gearsets are attractive for power dense applications and concentric shaft layouts. This notebook reviews the unique geometric attributes of planetary gears and their significance to planetary gear mesh operation.

Gear geometry measurements are an important aspect of gear manufacturing and testing. Measurements of gear geometry are done for gear manufacturing to ensure quality criteria are met. Measurements are also performed for gear testing, such as design of experiments, to understand the influence of gear parameters on measured data. This notebook reviews the different types of gear geometry measurements commonly used in industry. This notebook is seeking author contributions.

Gear geometric quality, as quantitatively assessed by ISO and AGMA standards, is reviewed. Parametrically, gear quality is understood in the profile, helix, and radial directions. Gear quality is important to gear mesh operation, such as tooth load sharing and conjugate action. An increase in stresses, noise, and vibrations will occur with poor gear quality. Examples are provided for gear tolerances calculated per ISO and AGMA standards. This notebook is seeking author contributions.

Gear microgeometry of spur and helical gears is reviewed. Microgeometry is applied to the flanks of gear teeth as a finishing process during gear manufacturing, i.e. after the gear teeth are cut. Flank modifications resulting from this process are on the order of micrometers. The purpose of microgeometry modifications is to improve gear mesh operation, such as conjugate action and avoidance of tooth interferences. This notebook reviews the parameters of gear microgeometry and their significance to gear mesh operation. This notebook is seeking author contributions.

Learn about basic racks and their significance to manufacturing of cylindrical involute gears. A basic rack defines the tooth profile of a gear with infinite diameter and forms the basis of a family of gears. A basic rack is merely a set of geometric properties for describing gear tooth proportions. It is particularly useful for defining the parameters of a generating cutting tool capable of manufacturing cylindrical involute gears.

Learn about rack generation gear cutting methods to manufacture spur gears and helical gears. Hobs and rack cutters are rack generation tools commonly used in the gear industry. Gear hobbing uses rotational motion to efficiently and accurately cut gear teeth. Gear tooth geometry, especially the root fillet, depends on the hob geometry and machining settings. This notebook is seeking author contributions.

Learn about pinion generation gear cutting methods to manufacture spur gears, helical gears, and internal gears. Pinion cutters, or shapers, are pinion generation tools commonly used in the gear industry. Unlike rack generation, gear shapers can also cut internal gears, also known as ring or annulus gears. Gear tooth geometry, especially the root fillet, depends on the shaper geometry and maching settings. This notebook is seeking author contributions.

Learn to calculate gear forces in parallel axis spur and helical gears. Spur gears only generate forces in the gear plane, however helical gears generate an axial force component therefore need to be supported axially as well. Tangential and radial forces in the gear plane cause bending moments on the supporting shafts. Axial force generates bending in the perpendicular plane. So the calculation of gear forces is important in design of shafts and bearings.

Learn to calculate root bending stress in parallel-axis spur gears. A gear tooth can be modeled as a cantilever beam under load. Gear tooth bending was first investigated by Wilfred Lewis, and the bending stress equation is referred as the Lewis formula. This notebook documents the procedure to find spur gear root bending stress, given inputs of gear macro-geometry and applied torque.

Learn to calculate gear tooth contact stress in parallel-axis spur gears. Gear tooth contact along the tooth surface can be considered as a line. The width of the contact is much shorter than the length along the line of contact. The radius of curvatures of the contacting surfaces vary as the gears rotate. Maximum subsurface shear stress is just below the point of contact. This notebook documents the procedure to find spur gear contact stress, given inputs of gear macro-geometry and applied torque.

Learn about the rating of gear tooth bending strength according to ISO 6336-3. This notebook is seeking author contributions.

Learn about the rating of gear surface pitting durability according to ISO 6336-2. This notebook is seeking author contributions.

Learn about the rating of gear tooth bending strength according to AGMA 2001-D04. This notebook is seeking author contributions.

Learn about the rating of gear pitting resistance according to AGMA 2001-D04. This notebook is seeking author contributions.