Geometry / Involute¶

Description: Mathematical review of the involute curve and its significance to mechanical gear systems.

Table of Contents¶

Introduction
Mathematics
1. Parametric Curve
2. Curvature
Gearing
References

Introduction¶

An involute, specifically a circle involute, is a geometric curve that can be described by the trace of unwrapping a taut string which is tangent to a circle, known as the base circle.

The circle involute has attributes that are critically important to the application of mechanical gears.

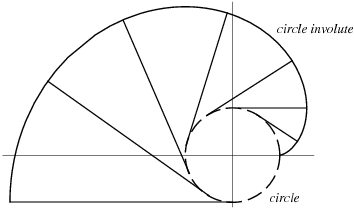
Circle involute curve

Circle involute from an unwrapped string

Image credit: Wolfram MathWorld

Mathematics¶

The mathematics of a circle involute curve is reviewed here.

Nomenclature¶

Symbol	Description
$r_b$	Base radius
$\psi$	Roll angle
$x$	Cartesian x-coodinate
$y$	Cartesian y-coordinate
$\kappa$	Curvature
$R$	Radius of curvature
$\alpha$	Pressure angle
$\text{inv }\alpha$	Involute function of pressure angle $\alpha$

Parametric Curve¶

An involute curve can be expressed by parametric equations in planar coordinates.

$$x = r_b (\cos\psi + \psi \sin\psi)$$$$y = r_b (\sin\psi - \psi \cos\psi)$$

These equations specifically define an involute for a circle positioned at (0, 0) and the involute base starting at a polar angle of zero in the $xy$ plane

Curvature¶

The curvature, $\kappa$, of any point on a curve is defined as the reciprocal of the radius of curvature, $R$, at that point.

$$\kappa = \frac{1}{R}$$

For a circle involute, the center of curvature and radius of curvature at any point is apparent based on its construction via an unwrapping string. Center of curvature always lies on the base circle, making the radius of curvature equal to roll distance.

The curvature of an involute is an important factor in the gear tooth stresses observed in a meshing gear pair.

Gearing¶

The involute is important to mechanical gears because it enables the transfer of mechanical power between rotating bodies without relying on friction as the mechanism of torque transfer, such as a car tire on a road surface. Furthermore, the rotational speed and torque can be modified during this transfer of power, enabling gear systems to change speed and torque between different points in the system.

INVOLUTE GEARS IN 4-SPEED TRANSMISSION

Involute gearing modeled in Gears App

Pressure Angle¶

The pressure angle for an arbitrary point on an involute curve is the angle between its radius vector and line tangent to the involute. As evident in the figure below, the involute base radius is related to the pressure angle at an arbiturary radius on the involute curve.

$$ r_b = r \cos\alpha $$

The pressure angle of an involute is important to how gears transfer mechanical power, including how the forces resolve on the gear teeth.

Involute parameters

Involute curve diagram

Involute Function¶

The involute function is mathematically expressed as a function of pressure angle.

$$\text{inv }\alpha = \tan\alpha - \alpha$$

The involute function can also be used to express the relationship between pressure angle and roll angle. The previous figure illustrates the involute function in the context of the roll angle and pressure angle.

$$\text{inv }\alpha = \psi - \alpha$$

The involute function and its inverse are useful for calculating parameters of involute gearing, as demonstrated in other notebooks.

Line of Action¶

The line of action refers to the line along which force is applied during the mating of involutes, such as meshing spur gears. This line is also be referred to as the pressure line or generating line. To understand the line of action, we must introduce the pitch circle and pitch point.

Pitch circle: Circle along which the involute body, e.g. gear, rotates without slip with a mating involute body.

Pitch point: Point along the line of action that intersects the pitch circle.

In the case of helical gearing, a plane of action must be considered since the involute teeth vary along the gear facewidth, causing the pressure angle at each point of contact to differ. For spur gearing, a plane of action also exists, but its involute teeth do not vary along the facewidth.^✝

✝ Ignoring any microgeometry modifications.

Conjugate Action¶

A key characterstic of involute gearing is conjugate action. Conjugate action results in a constant, i.e. non-flucuating, angular velocity relationship between the two rotating bodies involved. In the case of involute gearing, this constant angular velocity relationship corresponds to the gear ratio.

A gear pair with mating involute curves achieves conjugate action if the gear teeth have perfect involute geometry and are completely rigid and smooth. The animation below illustrates how the point of contact moves along the line of action for mating involute curves with conjugate action.

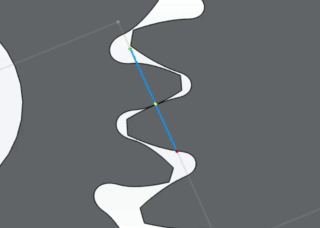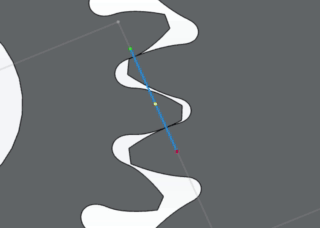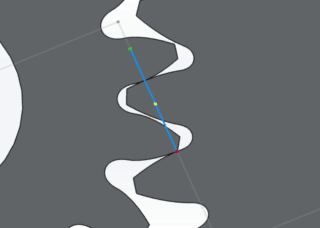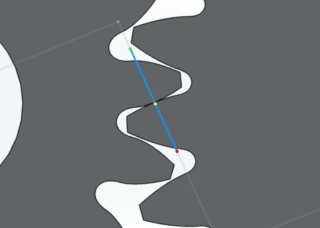
Involute parameters

Gear mesh line of action in Gears App

Actual gears are never manufactured with perfect involutes, and therefore nominal conjugate action is not achieved. In this case, the two gear bodies will have an angular velocity that fluctuates about its nominal constant value.

The figure below provides a qualitative demonstratration of the influence of imperfect involute geometry on the conjugate action of a gear mesh.

Lastly, even if gears were manufactured perfectly, they will not have conjugate action when loaded, i.e. when the gear teeth are acted upon by a force. Such phenomena are explained in later chapters by gaining an understanding of the forces acting on gear teeth, the elastic properties of gear teeth, and the kinematics of a gear pair.

Model Gears

Gears App software is used to accurately model, analyze, and build cylindrical involute gear systems entirely from your web browser.

Learn More

Notebook Series is free to learn and contribute knowledge about gears, such as geometry, manufacturing, strength, and more.

Edit Notebook

GitHub repos are used to publicly host our notebooks, allowing anyone to view and propose edits.